5. 동차좌표계

3차원 물체의 표현

3차원 물체는 곡면으로 이루어져있으며, 이 곡면은 수많은 평면 다각형으로 구성되어있다. 이 평면 다각형을 메시(Mesh), 표면 메시(Surface Mesh) 등으로 부르는데, 보통은 삼각형을 사용한다.

렌더링은 두 종류로 나뉜다.

  • 솔리드 렌더링 → 메시에 조명을 가하여 표면이 드러난 물체를 표현.
  • 와이어프레임 렌더링 → 메시의 경계선만으로 물체를 표현.

벡터 표시

그래픽에서는 물체 표현에 있어 다양한 수학적 요소를 사용하는데, 기본이 되는 것이 벡터이다. 벡터 공간(Vector space)이란, 주어진 벡터로부터 파생되는 모든 벡터의 집합을 의미한다. 주어진 벡터에 스칼라를 곱하거나 벡터끼리의 합성에 의해 만들어지는 모든 벡터의 집합인 것이다.

이러한 벡터를 3차원 공간상에 표현하려면 점(Point)이 필요하다. 점이 없다면 크기와 방향이 같은 벡터들은 모두 동일하게 취급 되기 때문이다. 점은 위치만 있고 크기와 방향은 없는 요소이므로, 벡터와 함께 사용하면 크기, 위치, 방향을 모두 표시할 수 있게 된다.

어파인 공간(Affine Space)은 점을 벡터처럼 취급하여 벡터 공간을 확장한 공간이다.

  • 벡터와 벡터 사이의 연산 → 벡터공간에서도 가능
  • 스칼라와 벡터의 연산 → 벡터공간에서도 가능
  • 점과 벡터의 연산 → 어파인 공간에서 가능

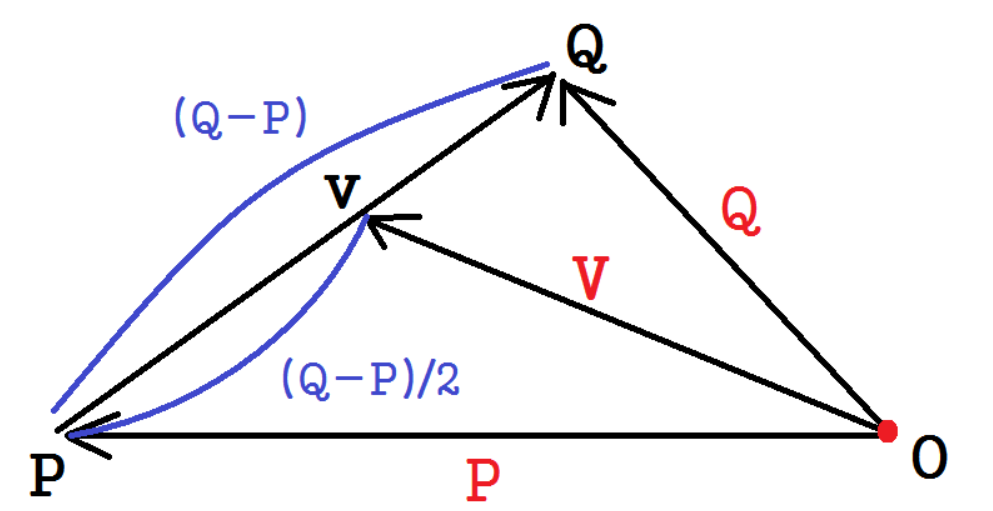
Untitled

예를 들어 점P(검정색P) = 원점에서 점P로 가는 벡터 P(빨간색P)로 표현할 수 있다. 벡터OP = P-O라고 표현할 수 있는 것과 같다.

동차좌표계(Homogeneous Coordinates)

3차원 공간에서 점이나 벡터를 어떻게 표현할 수 있을까? 단위벡터를 사용한다면 아래와 같을 것이다.

  • 벡터 v = 4i + 3j + 2k
  • 점 p = r + 4i + 3j + 2k (r = 임의의 시작점)

시작점 r의 유무에 따라 점과 벡터 표시가 달라지는 것이다. r이 없다면 두 표시는 모두 같아지게 된다. 이를 구분할 때 등장하는 것이 동차 좌표계이다.

동차 좌표계는 n차원 좌표를 n개 요소가 아닌 n+1개 요소로 표현한다.

  • 벡터 v = 4i + 3j + 2k + r·0 (4,3,2,0)
  • 점 p = 4i + 3j + 2k + r·1 (4,3,2,1)

3차원 벡터를 4개 요소로 표현한 모습이다. 마지막 요소가 0이면 벡터를, 0이 아니면 점을 의미한다.

왜 렌더링 파이프라인에서 동차 좌표계를 사용할까?

  • 3차원에서 정의된 공간을 2차원에 투영하고, 그 이미지를 얻기 위해서.
  • 3차원 공간의 affine 변환들을 모두 4x4 행렬로 변환하기 위해서.

점이나 벡터의 이동(Translation)을 생각해보자. 일반적으로 점 x1을 점 x2로 이동하려면 그 차이만큼의 값을 더해주면 된다. x1 + xΔ = x2의 형태이며, 행렬의 덧셈이다.

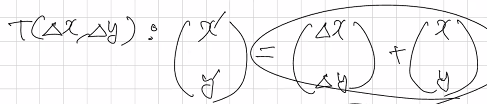
Untitled

다른 변환인 회전(Rotation), 확대(축소)는 모두 행렬 곱을 사용한다. 파이프라인 에서 다른 연산이 끼어있으면 변환이 복잡해지니 행렬 덧셈을 곱셈으로 전환해야 하는데, 이 때 동차좌표계가 사용된다.

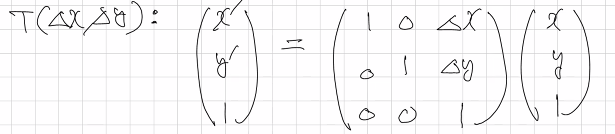
Untitled

이렇게 표현하면, 행렬 곱셈 형태이면서도 기존의 x1 + xΔ = x2를 지킬 수 있다. 2차원 공간이기에 3x3행렬이 나왔지만, 3차원 공간이면 4x4행렬로 만들 수 있다.

3차원 공간을 2차원에 투영한다는 것은 무슨 의미일까?

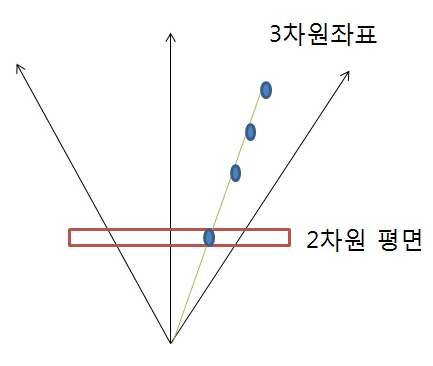
Untitled

2차원의 점(1,2)을 생각해보자. 이는 동차 좌표계로 (1,2,1)이다. 3차원 공간상에서 원점으로부터 (1,2,1)을 통과하는 직선이라고 볼 수 있다. 이 직선상의 점들은 (1,2,1), (3,6,3), (10,20,10)등의 값을 가지는데, 끝자리가 1이 되도록 규모를 줄인([x,y,z]라면 [x/z, y/z, 1]로 변경)후 1을 떼어내면 2차원 평면상의 점이 된다. 3차원을 2차원에 투영한 것이다.

참고자료