7. 좌표계 변환

좌표계의 종류

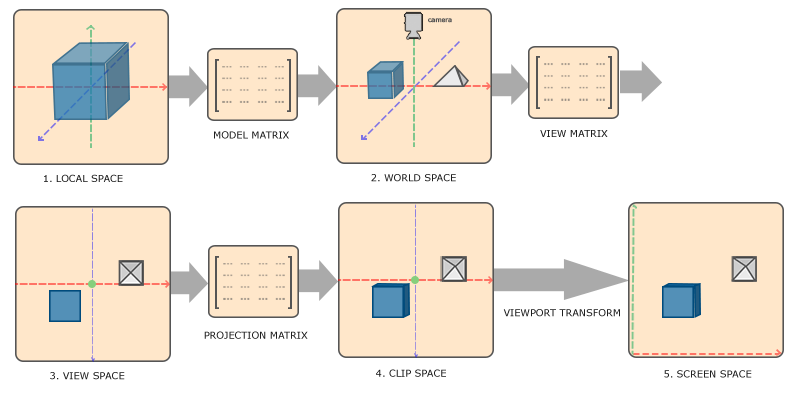
Untitled

위의 이미지는 3차원 공간을 2차원 화면으로 변환하는 과정을 나타낸다. 4→5번은 뷰포트 변환의 내용이므로 다음에 다루고, 우선은 나머지 좌표계 사이의 변환을 알아보자. 변환에 사용되는 좌표계는 아래와 같다.

  • 모델좌표계(=지역좌표계, Model Coordinate System)
  • 전역좌표계(=월드좌표계, World Coordinate System)
  • 시점좌표계(View Coordinate System)

물체가 처음 등장했을 때, 물체의 각 요소는 모델 좌표계에 정의되어있다. 이 좌표계에 변환행렬을 곱하여 전역좌표계로 변환하는데, 이 과정을 통해 여러 물체 각각의 좌표계를 전역좌표계로 통일할 수 있다. 이후에 다른 변환행렬을 한번 더 곱하여 시점 좌표계로 전환한다. 시점좌표계는 우리의 눈 혹은 카메라에 해당하며, 카메라의 위치에서 물체들이 어떻게 보이는지를 나타낸다.

행렬 스택

각 좌표계에서의 점과 벡터는 행렬의 형태로 표시되며, 행렬의 연산을 통해 좌표계간의 변환이 이루어진다. 이 때 행렬의 연산은 스택(stack)에 누적 되며, 각 스택의 요소는 구분되어 있으므로 기존의 행렬에 영향을 미치지 않고 새로운 연산이 가능하다.

  • glPushMatrix()
  • glPopMatrix()

새로운 행렬을 추가(push) → 연산 → 행렬 제거(pop)의 순서로 진행된다.

계층 구조의 표현에는 두 가지 방법이 있다.

  • 순방향 키네마틱스(Forward Kinematics) → 상위에서 하위로 동작을 구현
  • 역방향 키네마틱스(Inverse Kinematics) → 하위에서 상위로 동작을 구현

설명을 위해서 다리를 생각해보자. 몸통, 허벅지, 종아리, 발 순서대로 계층적 구조를 이룬다. 허벅지가 움직이면 그 아래 달린 종아리와 발도 함께 움직이는 것이다.

순방향 키네마틱스는 이러한 계층을 계층의 상위부터 그려낸다.

  1. 몸통 연산 후 스택에 행렬을 push
  2. 허벅지 연산 후 스택에 행렬을 push
  3. 종아리 연산 후 스택에 행렬을 push
  4. 발을 그린다.
  5. 4→3→2→1의 순서로 행렬이 pop된다.

이와 같은 과정은 원하는 자세를 섬세하게 조절할 수 있다는 장점이 있지만, 사용자가 각 관절의 변환을 입력해야하기에 번거로움이 있다.

역방향 키네마틱스는 반대로 계층구조의 하위부터 그려내는 방법이다. 순방향 키네마틱스와는 다르게 상위 부분을 컴퓨터가 알아서 계산한다. 발의 위치와 각도를 조절하면, 관절의 범위 내에서 종아리, 허벅지, 몸통등이 그려진다는 것이다. 그러나 해당 범위 내에서 여러 자세가 나올 수 있으므로, 여러 제약조건을 통해 원하는 자세가 되도록 설정해야 한다.

모델-전역 좌표계 변환

$P’ = M\cdot P$ 라는 행렬곱을 생각하자. 이때 M은 여러 행렬의 곱이다.

  • P’ = 전역좌표
  • M = 변환행렬
  • P = 모델좌표

다르게 표시하면 $CTM = I\cdot S\cdot R\cdot P$ 의 모습으로 표현할 수도 있다.

  • CTM = 현재 스택의 가장 위에 있는 행렬
  • I = 단위행렬. 다른 행렬들을 곱하기 위한 모판
  • S, R, T = 변환 연산

새로운 변환은 우측에 추가된다. 연산은 우측부터 좌측으로 P→R→S의 순서로 진행된다.

전역-시점 좌표계 변환

모델좌표계에 모델 행렬glScalef(), glRotatef(), glTranslatef()을 곱하면 전역좌표계가 되는 것 처럼, 전역좌표계에 뷰행렬glLookAt()을 곱하면 시점좌표계가 된다.

카메라 좌표계는 여러 종류가 있다. GKS, PHIGS와 같은 그래픽스 국제 표준이 이에 해당한다. 이들은 전문적이지만 변수가 많아서 사용하기가 어려우므로, OpenGL은 이들을 간편화하여 3가지 요소로 시점좌표계를 결정한다.

  • 카메라 위치
  • 카메라가 바라보는 점(초점)
  • 카메라 기울임

그 결과가 void gluLookAt()이다. 무려 9개의 파라미터가 있는데, 위의 3가지 요소에서 x, y, z방향을 나타내는 것이다. 참고로 파라미터는 전역 좌표계이다.

참고자료