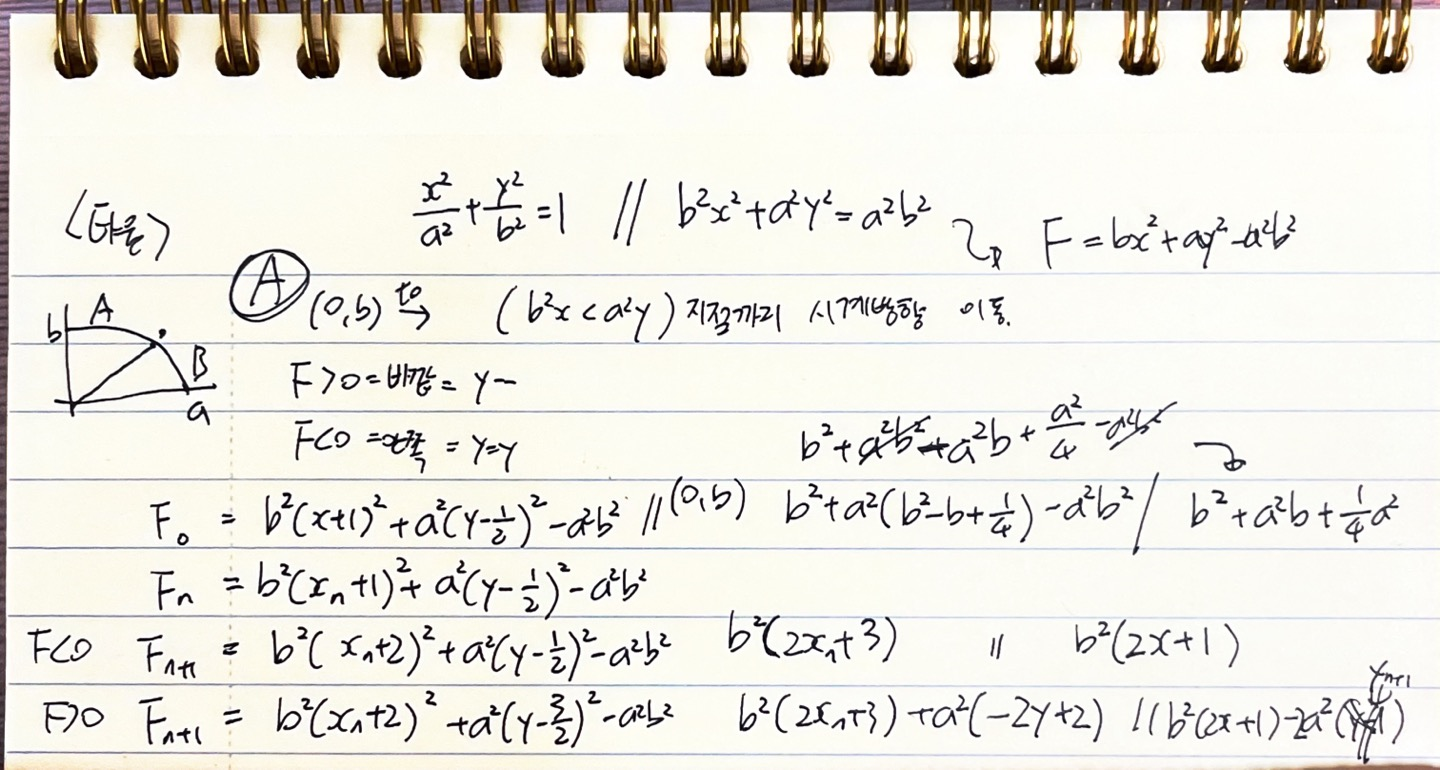Bresenham 알고리즘으로 타원 그리기
Bresenham 알고리즘을 타원에 적용하는 방법
4. Bresenham 알고리즘으로 타원 그리기
타원은 어떻게 그릴까
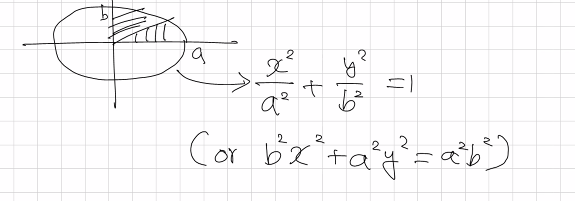
타원 또한 원처럼 2차식이다. 앞에서 원을 그려보았다면 비교적 수월하게 가능하다. 타원과 원의 차이점은 1/8원을 그려서 평행이동이 불가능하다는 것이다.
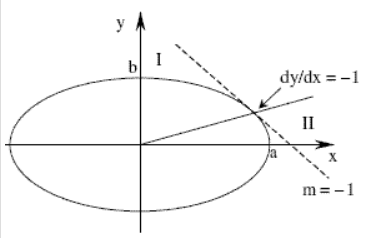
그러나 타원의 한 쪽 사분면을 절반으로 나누고, 각각의 부분을 평행이동 한다면 타원을 그릴 수 있다. 경계를 기준으로 윗부분은 Region1, 아랫부분은 Region2로 구분하겠다.
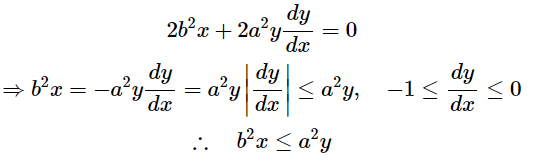
구분선은 접선의 기울기 = -1인 점을 기준으로 한다. Region1, Region2를 그릴 범위는 타원의 식을 미분하여 구했다.
Region1→ (0, b)에서 시계방향으로 내려간다.Region2→ (a, 0)에서 반시계 방향으로 올라간다.
브레젠험 알고리즘을 타원에 적용하기
범위를 구했으니, 각 범위에서 브레젠험 알고리즘을 적용해야 한다. 우선 판별식을 구해보자.
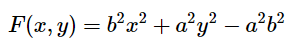
F(x,y) < 0→ 점(x, y)는 타원 내부에 존재한다.F(x,y) > 0→ 점(x, y)는 타원 외부에 존재한다F(x,y) = 0→ 점(x, y)는 타원 둘레에 존재한다
판별식은 타원 전체에 동일하게 작용하지만, 중단점과 그에 따른 변화는 Region1, Region2가 다르다. 우선은 Region1부터 진행하자.
Region1 → (0,b)에서 시계 방향으로 내려가기
x의 값은 1씩 증가하고, y값은 판별식에 따라 결정할 것이다. 다음 점을 그리기 위해 판별식에 값을 대입해보자. $F(x+1, y-0.5)$의 결과는 아래와 같다.
F > 0→ 중간점이 타원의 바깥쪽이다. → y = y -1F < 0→ 중간점이 타원의 안쪽이다 → y값 유지
판별식은 원을 그릴 때 처럼 조건에 따라 값이 변화된다. 이 작업은 조금 미뤄두고, 우선 시작점에서의 판별식 값을 구해보자. 시작점은 (0, b)이다.
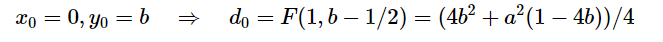
살짝 정리하면 $F_0 = b^2+0.25a^2-a^2b$ 라고 할 수 있다.
이제 조건에 따른 판별식 값의 변화를 생각해보자. y = y or y -= 1에 따라서 두 번째 판별식에 대입되는 중간점의 값이 달라진다.
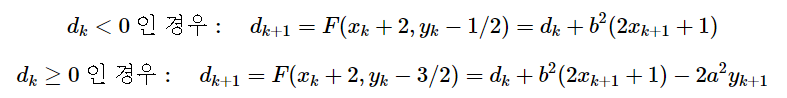
이제 구할 내용은 전부 구했으니 코드를 작성해보자.
// Region 1 -> (0, b)에서 시계방향으로 내려간다.
int a = 80;
int b = 60;
int F1 = b * b + 0.25 * a * a - a * a * b;
//int F1 = (4 * b * b + a * a * (1 - 4 * b)) / 4;
int x = 0;
int y = b;
glColor3d(0.0, 1.0, 0.0);
while (b * b * x < a * a * y) {
++x;
if (F1 < 0) {
F1 += b * b * (2 * x + 1);
}
else {
--y;
F1 += b * b * (2 * x + 1) - 2 * a * a * y;
}
plot4(x, y); // 4분면에 각각 점을 찍는다.
}
Region2 → (a, 0)에서 반시계 방향으로 올라오기
y의 값을 1씩 증가시키고, x값은 판별식에 따라서 유지하거나 감소시킨다. 대략적인 과정은 Region1에서 설명했으니 간단하게 짚고 넘어가자.
판별식은 동일하지만 그 결과가 달라지는 모습이다.
F > 0→ 중간점이 타원의 바깥쪽이다. → x = x -1F < 0→ 중간점이 타원의 안쪽이다 → x값 유지
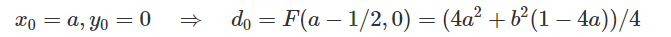
시작점에서의 판별식은 a, b의 위치를 바꾼 것에 지나지 않는다. $F_0 = a^2+0.25b^2-b^2a$ 와 같다.
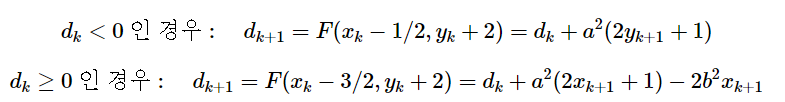
조건에 따른 판별식 값 변화 또한 크게 달라지는 내용은 없다. a, b위치만 잘 바꾸자. 코드는 아래와 같다.
// Region 2 -> (a, 0)에서 반시계방향으로 올라간다.
int a = 80;
int b = 60;
//int F2 = (4 * a * a + b * b * (1 - 4 * a)) / 4;
int F2 = a * a + 0.25 * b * b - b * b * a;
int x = a;
int y = 0;
glColor3d(0.0, 1.0, 0.0);
while (b * b * x > a * a * y) {
++y;
if (F2 < 0) {
F2 += a * a * (2 * y + 1);
}
else {
--x;
F2 += (-2) * b * b * x + a * a * (2 * y + 1);
}
plot4(x, y); // 4분면에 각각 점을 찍는다.
}
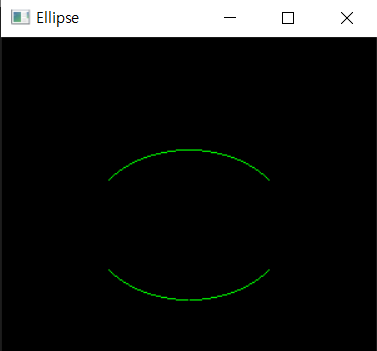
완성된 타원
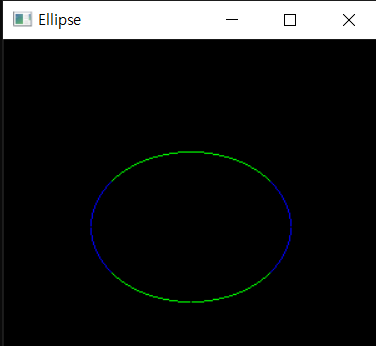
참고로 plot4()는 4분면에 각각 점을 찍는 함수이다.
void plot4(int x, int y) {
glVertex2i(x, y);
glVertex2i(-x, y);
glVertex2i(x, -y);
glVertex2i(-x, -y);
}
보기 힘들지만… 전체 계산 과정은 아래와 같다.