6. 기하 변환

2차원 변환

x, y값으로 이루어진 2차원 좌표계에서의 변환을 다룬다.

Untitled

  • 평행이동(Translation)
  • 크기변환(Scaling)
  • 회전(Rotation)
  • 비틀림(Shear)

평행이동

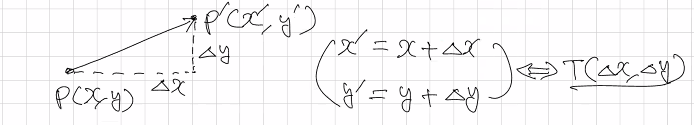
Untitled

위쪽의 그림은 일반적으로 표현한 평행이동이다. 기존 좌표(x, y)에 각각 변화량을 더하여 이동 좌표(x’, y’)를 얻는 것이다. 기호는 T(Δx, Δy) 이다.

크기변환

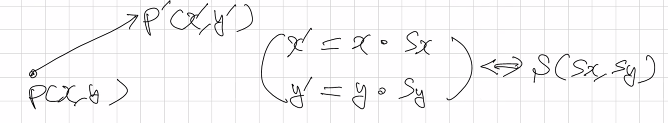
Untitled

기존 점에 스케일링 펙터(Sx, Sy)를 곱하여 이동 좌표를 얻는다. 기호는 S(Sx, Sy)이다.

회전

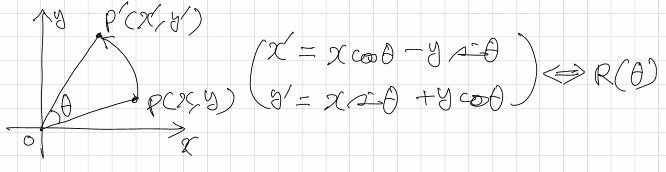
Untitled

원점을 기준으로 각도 $\theta$만큼 회전하여 이동 좌표를 얻으며, 기호는 R($\theta$)이다. 각도라는 특성상 삼각함수를 사용한다. 아래와 같은 식을 통해 구한다.

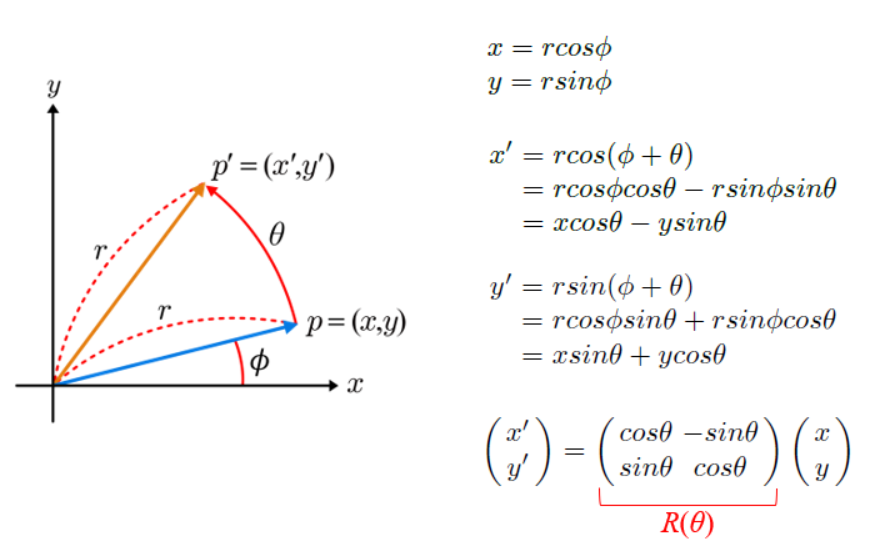
Untitled

*날림으로 적혔지만 sin, cos 이다…

비틀림

비틀림의 특징은 한쪽 축의 값은 유지하면서 다른 쪽 축의 값은 변한다는 것이다. x축, y축의 경우를 나눠서 생각해보자.

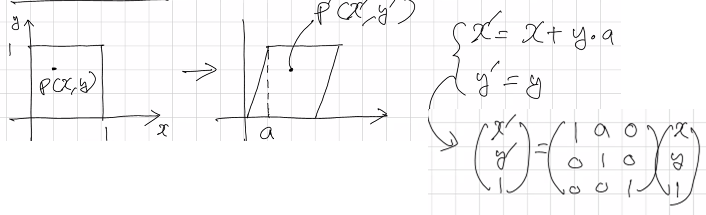
Untitled

x축의 경우, y값은 동일하지만 x값에 변화가 생겼다. 위에서부터 아래까지 균일하게 밀린 것이 아니므로, 위와 같이 표시한다.

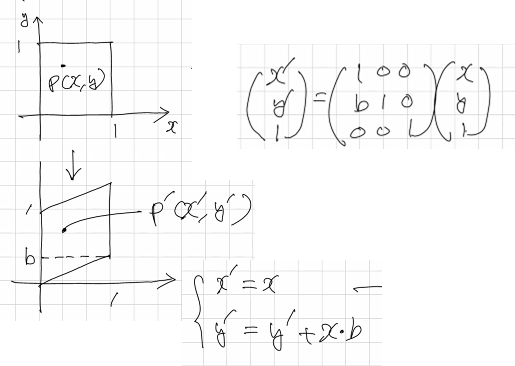
Untitled

y축의 경우도 x축의 경우와 비슷하다.

행렬로 변환 나타내기

위에서는 일반적인 식으로 각 변환을 표시하였지만, 컴퓨터에서 이들을 연산하기 위해서는 행렬로 나타낼 필요가 있다.

  • 평행이동

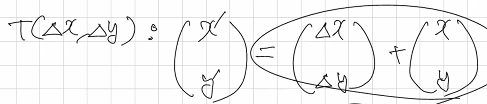
    Untitled

  • 크기변환

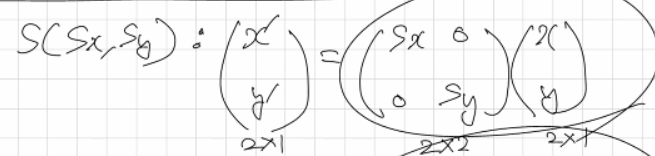
    Untitled

  • 회전

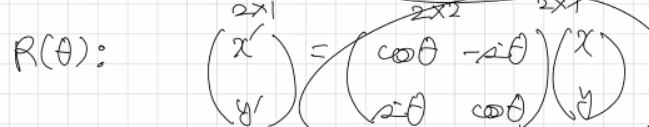
    Untitled

이 때 문제가 되는 부분은 평행이동이다. 크기변환, 회전은 모두 행렬곱의 형태인데 반하여 평행이동은 행렬 덧셈의 형태이기 때문이다. 컴퓨터가 이미지를 연속적으로 계산하기 위해서는 행렬의 곱셈 형태가 가장 적합하다.

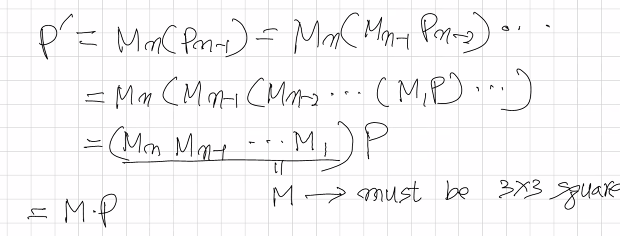
Untitled

위의 식을 보면, 원본 행렬 P에 변환 행렬 M을 순서대로 곱하여 결과 행렬 P’를 얻는 모습이 보인다. 저 사이에 행렬 덧셈이 끼면 어떻게 될까? 연산이 매우 복잡해질 것이다. 그렇기에 우리는 동차 좌표계를 사용하여 모든 연산을 정방 행렬로 표현한다. 동차좌표계에 관한 내용은 앞선 글을 참고하자.

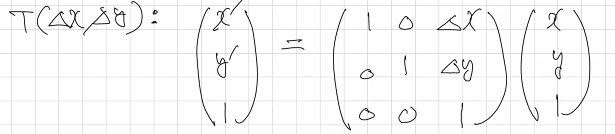
Untitled

이렇게 나타내면 식의 의미는 변하지 않은 채로 행렬 곱 연산이 가능하다.

3차원 변환

2차원 변환과 크게 다를 것은 없다. 다만 회전의 선택지가 늘어났다.

  • 평행이동

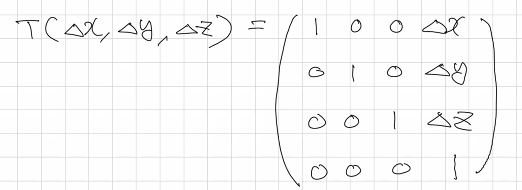
    Untitled

  • 크기변환

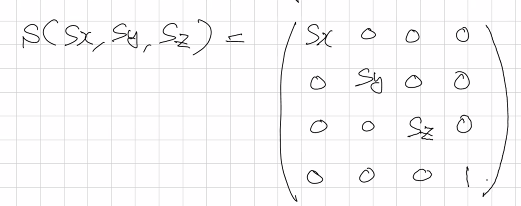
    Untitled

  • 회전 - x축

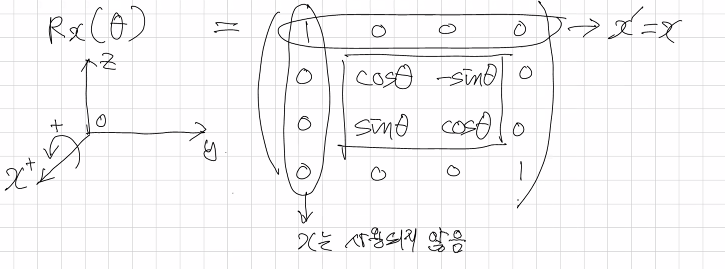
    Untitled

  • 회전 - y축

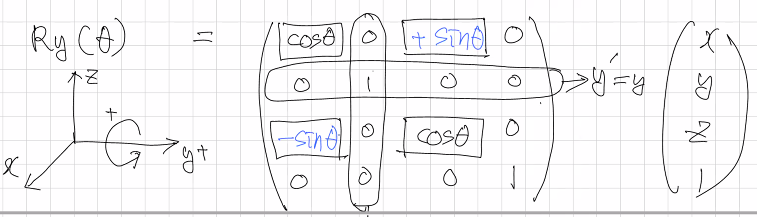
    Untitled

  • 회전 - z축

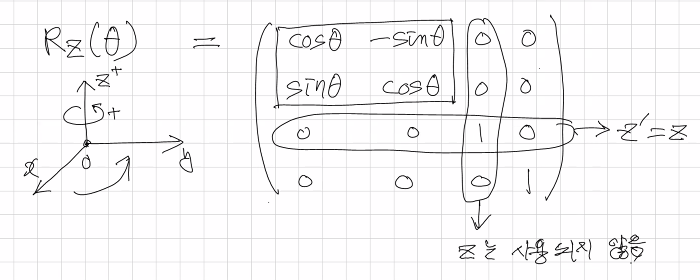
    Untitled

  • 회전 - 임의의 축

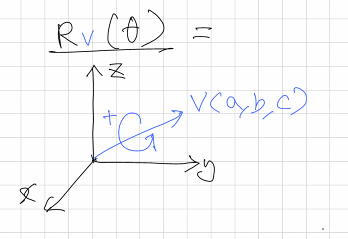
    Untitled

    임의의 벡터 v(a, b, c)를 기준으로 회전하는 동작이다. 순서는 다음과 같다.

    1. Z축을 기준으로 $\alpha$각도 만큼 회전한다.

      → 벡터 v를 z축 기준으로 회젼하여 zy평면 위로 올린다. v(0, ?, ?)

    2. X축을 기준으로 $\beta$각도 만큼 회전한다.

      → 벡터 v를 x축 기준으로 회전하여 z+축과 같아지도록 회전한다. v(0, 0, ?)

    3. Z축을 기준으로 처음에 원했던 $\theta$각도 만큼 회전한다.
    4. 2번, 1번 순서대로 $-\alpha, -\beta$각도 만큼 회전하여 복구한다.

참고자료