Bresenham 알고리즘으로 원 그리기
bresenham 알고리즘을 원에 적용하는 방법
3. Bresenham 알고리즘으로 원 그리기
원은 어떻게 그릴까
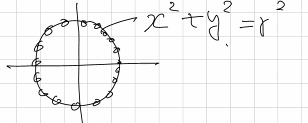
직선이야 기울기가 일정하니 시작점부터 끝점까지 쭉쭉 이어나가면 된다지만, 원은 기울기가 끊임없이 변하지 않는가? 직선과는 방식이 조금 다르다.
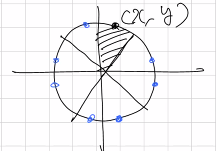
원을 8등분하여 한 조각에 해당하는 부분만 연산한 다음, 이에 대칭되는 점들만 찍는 일을 반복하면 된다.
#의사코드
plot8(x,y){ #8번 그리는 것을 그냥 하나의 함수로 합쳤다.
plot(x,y), plot(x,-y), plot(-x,y), plot(-x,-y),
plot(y,x), plot(y,-x), plot(-y,x), plot(-y,-x)
}
브레젠험 알고리즘을 원에 적용하기
차근차근 살펴보자. 직선을 구할 때는 0<기울기(m)<1 이었으므로, x를 증가시켰을 때 y+0.5를 검사했다. 하지만 원에서는 이야기가 조금 다르다.
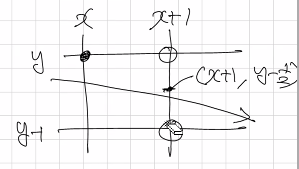
우리는 원의 가장 위쪽 점인 (0, r=반지름)에서 시작하여 시계 방향으로 1/8원을 그릴 것이다. x → x+1일 때 y는 감소하므로, 원의 y값이 y-0.5보다 큰지 작은지를 판별해야한다.
원의 공식은 $x^2+y^2 = r^2$이므로, 판별식은 $d = x^2+y^2-r^2$이다.
d > 0→ 점(x, y)가 원의 바깥에 존재한다.d < 0→ 점(x, y)가 원의 내부에 존재한다.d = 0→ 점(x, y)가 원의 둘레에 존재한다.
이 판별식에 중간점(x+1, y-0.5)를 대입하여, 중간점이 원의 안에 있는지 바깥에 있는지를 확인할 수 있다.
d > 0→ 원의 둘레 바깥에 중간점이 존재 → 다음 점에서y = y -1d < 0→ 원의 둘레 내부에 중간점이 존재 → 다음 점에서y = y
그 결과에 따라, 다음 점에서의 y값을 결정한다.
#의사코드
# '^'표시는 제곱을 의미한다.
x=0, y=r
while(x<y){
x=x+1
d=x^ + (y-0.5)^ -r^
if(d>0) y=y-1
plot8(x,y)
}
이를 기반으로 작성한 초기 코드이다. 각 요소는 다음과 같다.
x=0, y=r→ 알고리즘 시작점은 (0,r), 원의 가장 위쪽 지점이다.while(x<y){→ y=x 는 기울기가 1인 직선이다. 위쪽부터 1/8원을 그릴 것이기에 x<y 구간으로 한정한다.x=x+1→ x를 1씩 증가시켰을 때d=x^ + (y-0.5)^ -r^→ 해당 지점에서 중단점의 위치를 판별한다.if(d>0) y=y-1→ 중단점이 원의 바깥에 있으므로 y값을 낮춘다. 아니라면 그대로 y값을 유지한다.plot8(x,y)→ 이제 좌표를 찍을 점이 구해졌다.(x+1, y)or(x+1, y-1)이다. 해당 점을 포함하여, 대칭되는 8개 점을 그린다.
위의 코드는 동작하겠지만, 아무래도 제곱이 들어간 판별식을 반복하다보니 연산이 많다. 판별식을 반복문의 바깥으로 빼보자. d를 초기화 해야하니 최초의 d값을 구한다.
(0, r)에서 시작하는 원의 첫 번째 중단점은 (x+1, y-0.5)이다. 이를 판별식에 대입하면 $d = (x+1)^2 + (y-0.5)^2 - r^2$ 값이 나오고, 여기에 (0, r)을 대입하면 $1-r+1/4$가 구해진다. 참고로 1/4는 크기가 작아서 제거해도 별 영향이 없다.
판별식의 초기 값을 반복문의 바깥으로 뺐으니, 반복문 내부에서는 조건에 따라 이 값을 변화시켜야 한다. 주의할 점은 분기에 따라 y값이 다르다는 것이다.
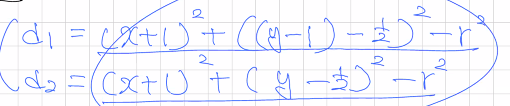
이전의 y값을 그대로 사용하는가, y=y-1인가에 따라서 위와 같은 식이 된다. 반복문에서 제곱을 제거하는 것이 목표이므로, d1, d2를 d의 초기값의 변형으로 나타내보자.
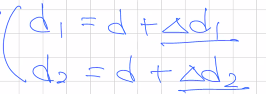
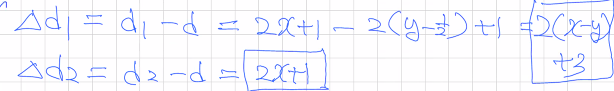
이렇게 구한 값은 모두 정수 연산이며, 곱연산 또한 2의 배수이므로 shift연산으로 변경할 수 있다. 이를 토대로 기존의 코드를 수정해보자.
#의사코드
x=0, y=r
d = 1-r
while(x<y){
x=x+1
if(d>0){ # 중간점이 원의 바깥에 있다. -> y값 감소
d=d+2(x-y)+3
y=y-1
}
else d=d+2x+1 # 중간점이 원의 내부에 있다 -> y값 유지
plot8(x,y)
}
실제 코드
#include <GL/glew.h>
#include <GL/glut.h>
#include <stdlib.h>
void plot8(int x, int y) {
glColor3d(0.0, 1.0, 0.0);
glVertex2i(+x, +y);
glVertex2i(-x, +y);
glVertex2i(+x, -y);
glVertex2i(-x, -y);
glVertex2i(+y, +x);
glVertex2i(-y, +x);
glVertex2i(+y, -x);
glVertex2i(-y, -x);
}
void circle() {
glClear(GL_COLOR_BUFFER_BIT);
glBegin(GL_POINTS);
int r = 50;
int x = 0;
int y = r;
int d = 1 - r;
while (x < y) {
++x;
if (d > 0) {
d += 2 * (x - y) + 3;
--y;
}
else {
d += 2 * x + 1;
}
plot8(x, y);
}
glEnd();
glFlush();
}
int main(int argc, char** argv) {
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH);
glutInitWindowPosition(300, 100);
glutInitWindowSize(301, 301);
glutCreateWindow("Circle");
glClearColor(0.0, 0.0, 0.0, 0.0);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glOrtho(-150.0, 150.0, -150.0, 150.0, -1.0, 1.0);
glutDisplayFunc(circle);
glutMainLoop();
return 0;
}
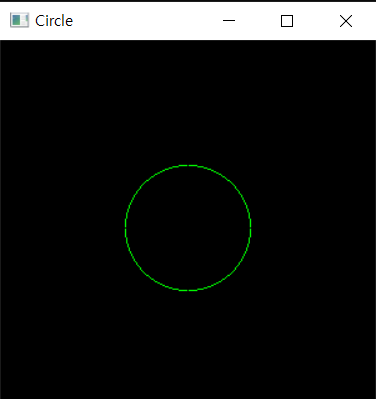
참고로 반복문 내의 if조건을 if(d > 0)에서 if(d < 0)으로 바꾸면 마름모가 나온다.
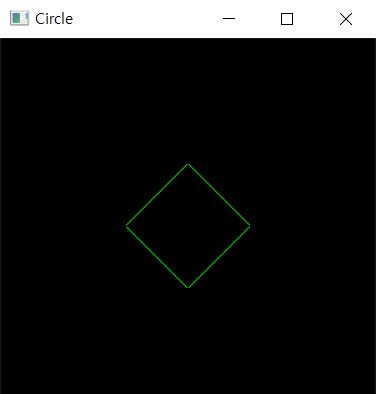
원의 둘레를 구성하는 각 점과 원점을 잇는 직선을 브레젠험 알고리즘으로 그린다면 이런 모양이 나온다.
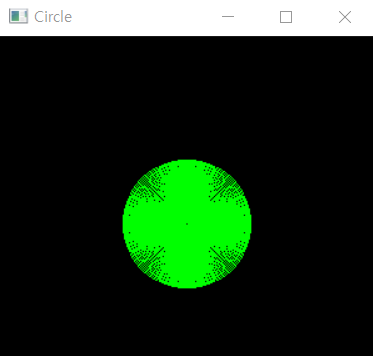
void bresenhamLine(int endX, int endY) {
int x = 0; // 직선의 시작점이 (0,0)임을 의미
int y = 0;
int W = endX; // 본래 endX - startX 지만, start지점이 원점이므로 끝점만 표시했다.
int H = endY;
int F = 2 * W - H;
int disF1 = 2 * W;
int disF2 = 2 * (W - H);
while(y <= endY) {
++y;
if (F < 0) {
F += disF1;
}
else {
F += disF2;
++x;
}
plot8(x, y);
}
}
// circle()의 반복문 가장 위쪽에 bresenhamLine(x, y); 추가하기.