윈도우 클리핑
Cohen-Satherland, Liang-Barsky, Sutherland-Hodgeman
8. 윈도우 클리핑
윈도우 클리핑이란?
화면상에 표현할 내용만을 표현하고, 겹치거나 잘려나가는 내용은 표현하지 않는 것을 의미한다.
위의 이미지와 같이 여러 창이 띄워져 있을 때, 겹쳐진 부분은 어떻게 디스플레이 하지 않을 수 있을까?
Line Clipping
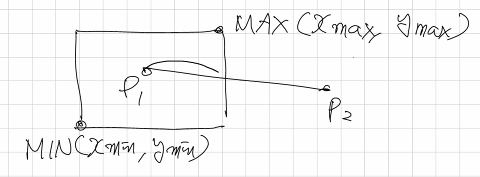
MIN, MAX 범위로 나타낼 수 있는 창에서, 두 점 p1(x1,y1)과 p2(x2,y2)를 잇는 선분의 일부만을 그리고자 한다. 두 가지 알고리즘이 있다.
- Cohen-Satherland Algorithm(코헨 서덜랜드 알고리즘)
- Liang-Barsky algorithm(리앙 바스키 알고리즘)
Cohen-Satherland Algorithm(코헨 서덜랜드 알고리즘)
윈도우 주변을 9개 영역으로 구별하고, 좌우상하를 의미하는 4bit의 아웃코드(l, r, t, b)로 나타내는 방식이다.
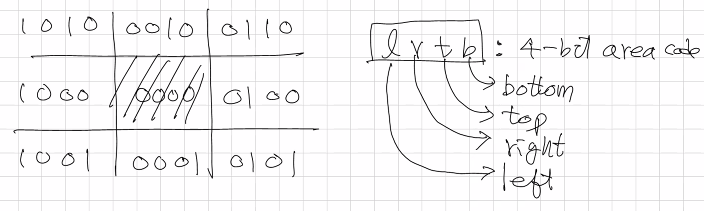
표현하고자 하는 선분의 양 끝점(P1, P2)의 코드를 연산하여 위치를 파악한다.
-
P1 & P2= 0000 (AND 연산)→ 두 점 모두 윈도우 중앙에 위치하므로 선분을 모두 표시한다.
-
P1 & P2≠ 0000 (AND 연산)→ 두 점 모두 윈도우 바깥에 있거나, 한 점이 윈도우 바깥에 존재한다. 어찌되었든 일부를 잘라내야 한다.
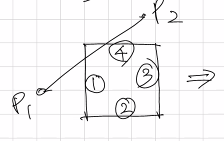
잘라내기는 위와 같이 윈도우의 각 변에 대하여 진행된다. 한쪽 변과 직선이 만나는 지점을 I로 지정하고, 그 바깥의 직선은 표시하지 않는 것이다.
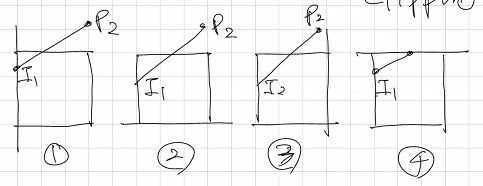
모든 변을 순회하고 나면 클리핑 된 선분만이 남는다.
Liang-Barsky algorithm(리앙 바스키 알고리즘)
선분을 매개변수(parameter) 방정식으로 표현한 후, 그 매개변수의 범위를 윈도우 범위에 맞추어 클리핑하는 알고리즘이다. 잠깐 선분을 매개변수로 나타내는 법을 돌아보고 가자.
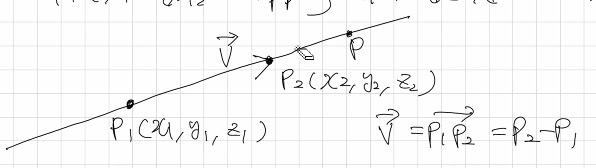
직선은 위와 같은 모양이다. 두 점, 그리고 두 점을 연결하는 직선상의 점 P가 있다.


점 P는 매개변수 t를 사용하여 표현할 수 있다. 이 때 t의 범위에 따라서 선분의 길이가 변한다.
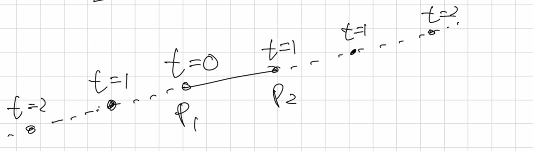
이 때 t의 범위가 [0, 1]이라면, 점 P는 선분 P1P2의 범위 내부에 존재한다고 할 수 있다.
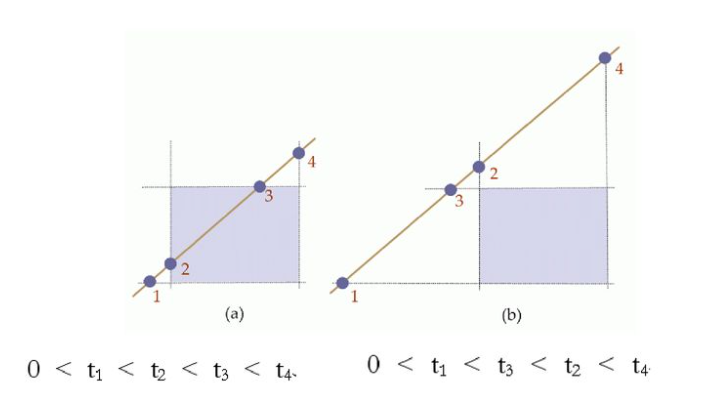
이제 윈도우에 이를 적용해보자. 선분은 윈도우 절단 사각형의 모든 변을 대상으로 교차점을 계산한다. 그리고 교차점의 t값을 계산하는데, 위의 이미지처럼 t값의 순서가 뒤바뀌는 경우가 존재한다. 이러한 경우들을 종합적으로 판단하여 절단하는 것이 리앙 바스키 알고리즘이다.
Polygon Clipping
n-side polygon(n각형) 의 점들 <p1, p2….pn>에서, 윈도우 내부에 있는 부분만 잘라내서 그리는 방법이다. 참고로 폴리곤을 나타내는 방법은 여러가지가 있다.
- 정의
- Set of Edges → 선분의 집합으로 표현.
- Sequence and Vertices → 점들의 집합으로 표현
- 종류
- Convex → 볼록 다각형(ex: 오각형)
- Concave → 오목 다각형(ex: 화살표)
- Non-Simple → 중간에 크로스하거나 안쪽이 비어있는 다각형
- 자르는 방법
-
Line Clipping → 자르면 선이 남는다.

-
Area Clipping → 자르면 면이 남는다.

-
Sutherland-Hodgeman Algorithm(서덜랜드 호그맨)
다각형을 자르는 알고리즘이다. 다각형은 꼭짓점과 변으로 구성되는데, 아래와 같이 표시한다.
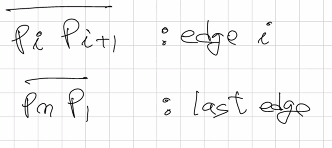
알고리즘은 다각형을 구성하는 각 꼭짓점들 <p1, p2, p3….pn>에 대하여 순차적으로 실행된다. i 번째 점에서 i+1번째 점으로 이동할 때 마다 윈도우를 벗어나는지 검사한다.

윈도우 내부에서 다각형이 그려진다면 현재의 점만을 표시하지만, 윈도우 바깥으로 나갈 때는 현재의 점과 점 I를 반환한다. 반대로 윈도우의 바깥에서 안으로 들어올 때는 점 I만을, 윈도우 바깥에서의 이동은 아무것도 반환하지 않는다.
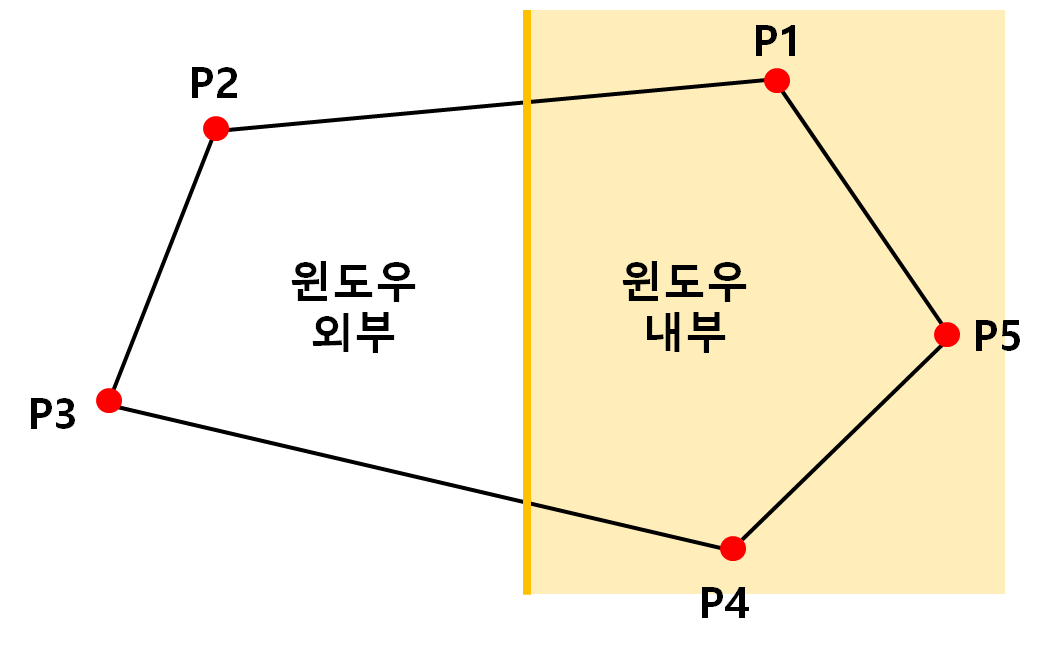
위와 같은 다각형을 예로 들어보자. 다각형은 <P1, P2, P3, P4, P5>로 구성되어있다. P1부터 시작하여 차례대로 검사를 진행한 결과는 아래와 같다.
- P1 → P2 : P1, I1 반환
- P2 → P3 : P1, 반환 x
- P3 → P4 : I2 반환
- P4 → P5 : P4 반환
- P5 → P1 : P5 반환
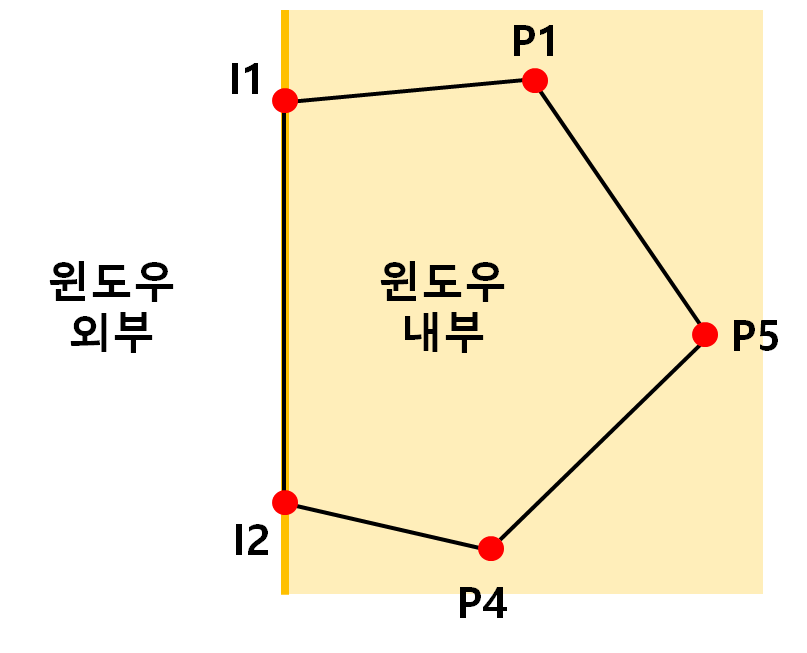
새로운 다각형 <P1, I1, I2, P4, P5>가 완성되었다.
참고 자료
- https://slidesplayer.org/slide/15028369/
- OpenGL로 배우는 3차원 컴퓨터 그래픽스(주우석, 한빛아카데미, 2013)