2. DDA와 Bresenham algorithm으로 직선 그리기

Line이란?

두 점 p1(x1,y1), p2(x2,y2)를 잇는 직선이다. 현실에서는 그냥 똑바로 연결하면 되지만, Raster graphic 환경에서는 여러 점(Pixel)들의 집합으로 직선을 그려야 한다. 직선은 아래의 특징을 가진다.

accurate ending(끝점은 정확해야하고)
straight(곧아야 하며)
even thickness(균일한 두께와)
continuous(연속적이어야한다)

픽셀을 이어서 그림을 그리다보면 뚜둑뚜둑 끊어질 텐데, 어떻게 직선을 그릴까.

DDA(Digital Differential Analyzer)

DDA는 분석을 통하여 직선의 다음 점을 어느 좌표에 찍을지 정하는 알고리즘이다.

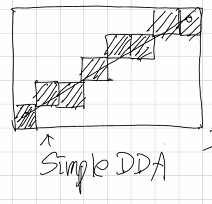
Untitled

한 좌표를 일정한 간격으로 이동하며 다른 좌표의 값을 계산하고, 이를 반올림하여 점을 찍을 좌표를 구한다. x축을 기준으로 보면 간단하다.

x좌표를 시작점부터 1씩 증가시킨다.
y좌표는 직선의 기울기만큼 더한 후, 이를 반올림 하여 정수를 구한다.
구한 (x, y)의 좌표에 점을 찍는다.

DDA의 문제는 직선의 기울기가 0<m<1일 때만 작동한다는 것이다. 해당 범위를 벗어나면 실수 연산을 하므로 연산 속도가 느려진다.

#의사코드
x=x1, y=y1 

while(x<x2){
	x = x + 1
	y = mx + b  //m, b는 실수. 실수연산은 속도 저하의 원인이다.
	plot(x, ㄴy) // y를 반올림 한 후 점을 찍는다. plot()은 점찍기함수.
}

브레젠험 알고리즘(Bresenham’s algorithm)

DDA의 문제점을 해결하고자 나온 것이 브레젠험 알고리즘이다. 실수 연산 없이 정수 연산만을 수행하여 속도가 빠르다. 구조는 대강 아래와 같다.

#의사코드
#미리 선언
c1 = 2Δy - Δx
c2 = 2Δy - 2Δx
c3 = 2Δy

#연산
x=x1, y=y1, plot(x,y)
**e=c1**
while(x < x2){
	x = x + 1
	if(e>0){ y = y+1; e=e+c2 }
	else{ e = e+c3 }
	plot(x,y)
}

#앞으로 계속 말할 내용
직선의 시작점(x1, y1)
직선의 끝점(x2, y2)
Δx = x2 - x1, Δy = y2 - y1
변수 x, y
직선 y=mx+b
e = 현재 점에서 직선의 y값 - 이전의 y값
plot(x,y) = 점 찍기 함수

어떻게 이런 결과가 나온걸까? 일단 직선(y=mx+b, 0<m<1)을 그려보며 알아보자. 직선 그리기의 기본은 DDA처럼 x값을 한 칸씩 이동하며 y값에 점을 찍는 것이다.

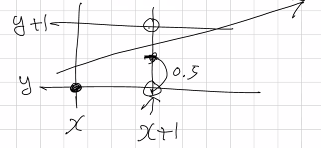
Untitled

우선 시작부분에 점을 찍는다. 그리고 x → x+1이 되었는데, y점은 어디 찍어야할까? 시작부분의 값인 y인가? 아니면 y+1인가?

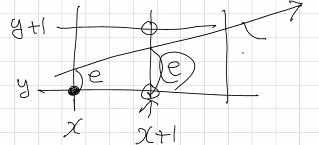
Untitled

그것은 그리려는 직선과 이전y값의 차이인 e로 판단한다. e값이 0.5보다 크다면 (x+1, y+1)지점에 점을 찍을 것이고, 0.5보다 작다면 그대로 (x+1, y)지점에 점을 찍을 것이다.

그리고 x, x+1모두 e라고 표시했는데, 앞과 뒤의 e는 기울기인 m만큼 차이가 난다(mx+b, m(x+1)+b). 따라서 아래와 같이 표현 가능하다.

#의사코드

#연산
while(x < x2){
	x = x+1
	e = e+m
	if(e>0.5){ y=y+1; e=e-1 }
	plot(x,y)
}

위의 식은 기본적인 기능을 제공하지만, m과 0.5라는 실수가 개입한다. 최소공배수를 양변에 곱해서 정수로 바꾸자. m = Δy/Δx이고 Δy, Δx각각은 정수이므로, 분모의 1/Δx와 0.5를 제거하기 위해 2Δx를 곱하면된다.

#의사코드
x=x1, y=y1 #시작점부터 대입
e=0 #시작점에서는 직선과 y값이 동일하다.

while(x < x2){
	x = x+1
	e = e+2Δy
	if(e > Δx) { y = y+1; e= e-2Δx }
	plot(x,y) 
}

여기서 식을 좀 더 간결하게 바꿀 수 있다. if의 내부를 보면 비교 연산을 진행하는데, 한 쪽을 0으로 만들어서 연산 속도를 높여보자.

#의사코드
x=x1, y=y, plot(x,y)
e=0

while(x < x2){
	x = x+1
	e = e+2Δy - Δx
	if(e > 0) { y = y+1; e= e-Δx }
	else{ e = e+Δx}
	plot(x,y) 
}

e = e+2Δy → e = e+2Δy - Δx, if내부 정리를 위해 Δx를 미리 뺐다.
if(e > Δx) → if(e > 0)
if 조건이 true 일 때 e= e-2Δx → e= e-Δx
if 조건이 false 일 때 e = e+Δx, 추가되었다.

이렇게 보니 반복문의 바깥으로 뺄 수 있는 내용들이 많다. e의 초기값도, Δy도, Δx도 알기 때문이다. 전부 바깥으로 빼서 정의해주면 처음에 보여준 브레젠험 알고리즘이 완성된다.

#의사코드
#미리 선언
c1 = 2Δy - Δx
c2 = 2Δy - 2Δx
c3 = 2Δy

#연산
x=x1, y=y1
e=c1

****while(x < x2){
	x = x + 1
	if(e>0){ y = y+1; e=e+c2 }
	else{ e = e+c3 }
	plot(x,y)
}

기울기에 따라서 x, y의 위치나 부호를 바꾸어주면 다양한 직선을 그릴 수 있다.

DDA와 Bresenham algorithm으로 직선 그리기

둘의 정의와 차이점

2. DDA와 Bresenham algorithm으로 직선 그리기

Line이란?

DDA(Digital Differential Analyzer)

브레젠험 알고리즘(Bresenham’s algorithm)

참고 자료