연속 행렬 곱셈 알고리즘

포스팅 이유

책의 설명은 이해가 잘 되지 않고, 블로그 설명은 책의 내용을 그대로 옮겨놓은 것들이 많았기 때문에 따로 정리하였다. 책이나 다른 사이트에서 “연속 행렬 곱셈” 글을 중심으로 학습하되, 내용을 이해하는데 도움이 되었으면 좋겠다.

연속 행렬 곱셈

행렬의 곱셈은 곱하는 순서에 따라서 전체 연산 횟수에 차이가 발생한다. 여기서 순서란 AB↔BA처럼 교환법칙을 의미하는 것이 아니다. AxBxC에서 AxB를 먼저할지, BxC를 먼저할지의 순서이다.

여기서 중요한 것은 ‘두 행렬을 곱하는 것의 반복’이라는 것이다. AxBxC에서 3개 행렬을 한 번에 곱하는 것이 아니다. (AxB)xC, Ax(BxC)처럼 순서가 다를 뿐 두 행렬의 곱이다.

행렬 곱셈 전체의 최소 연산 횟수와 그 순서를 구하기 위한 알고리즘을 알아보자.

코드

코드를 먼저 읽는 것도 좋지만 그림을 같이 보면서 이해하는 쪽이 개인적으 훨씬 편했다.

• An - 입력받은 행렬. 1~N까지 N개 존재.
• d - 각 행렬의 행 or 열. 행렬 A1의 경우 → 행:d0, 열:d1.
• C[i,j] - 행렬 Ai~Aj까지의 최소 연산 횟수. 아래 그림에서는 각 셀이 C에 해당하며, 그 좌표를 i, j로 나타낸다.

그림 설명

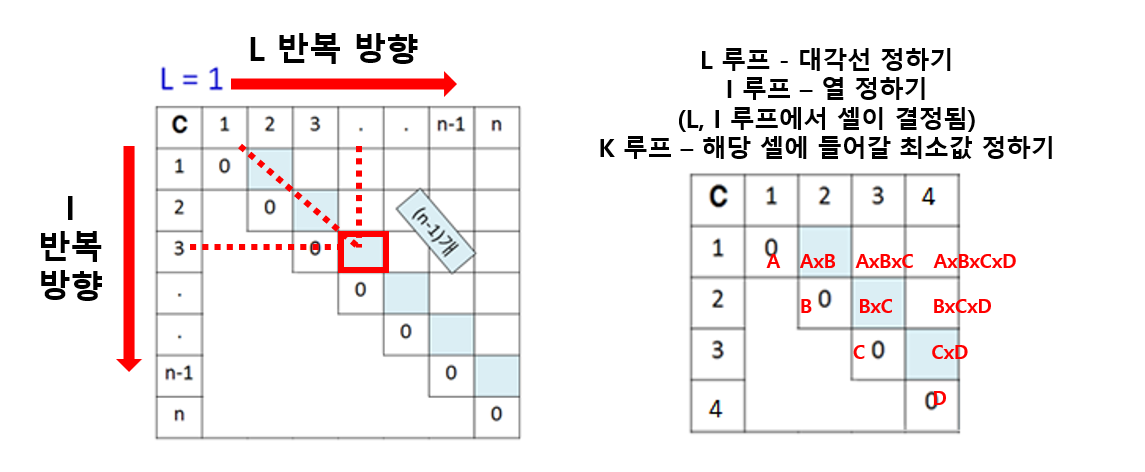
알고리즘은 L, i, k 루프를 반복하면서 각각의 셀 C[i,j]를 채워 나가는 과정이다. 최종 목적은 C[1, n]의 값을 구하는 것. 이는 행렬 A1~An까지 곱했을 때 최소 연산 횟수를 의미한다. 루프는 크게 세 과정으로 나뉜다.

• C[i,i]를 0으로 채움(줄:1~2)
• L, i 루프를 통해 표에서 셀을 순차적으로 선택
• k 루프를 통해 해당 셀에서 연산 최소 값 계산

각 루프를 알아보자.

L 루프

L은 부분 문제의 크기를 조절하는 인덱스라고 책에 적혀있다. L 자체가 부분 문제의 크기가 아니다! 그냥 인덱스다. 표에서는 대각선에 해당된다.

C[i,i]를 0으로 채우는 루프는 가장 긴 대각선을 채우는 과정이다. 다른 행렬과 곱하는 것이 아니라 그냥 행렬 본인이 부분문제인 A, B, C, D 이기에 값이 0이다.

L은 1부터 n-1까지 증가한다. L=0에 해당하는건 위의 루프에서 채웠기 때문. L→i→k 순서대로 루프가 진행되기에 위 이미지의 우측과 같은 순서로 계산이 진행된다. 대각선 하나→다음 대각선→다음 대각선이다.

i 루프

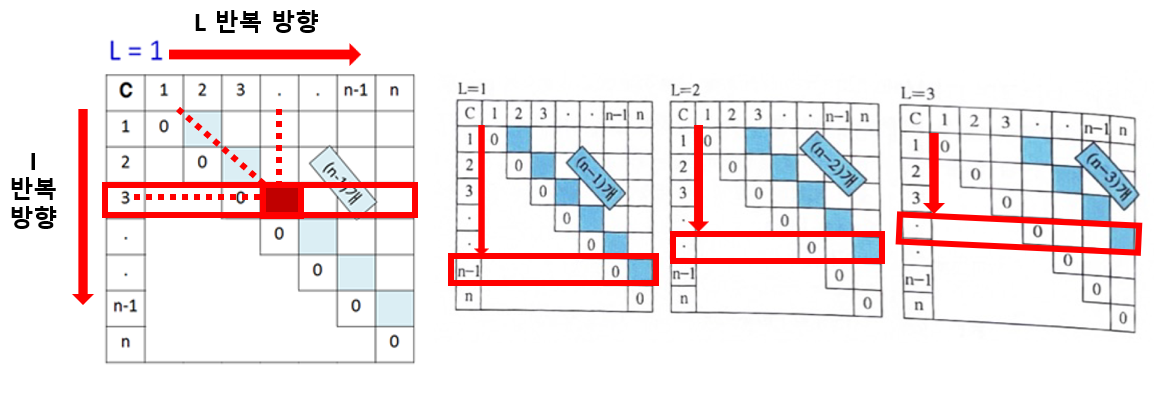
i루프는 행에 해당한다. L루프에서 대각선을 정했으니 i루프에서는 대각선에 있는 셀을 하나하나 선택하는 것이다.

i는 1부터 n-L까지 증가한다. L이 증가함에 따라 대각선의 길이가 점점 짧아지기 때문에(부분 문제의 개수가 줄어든다), 대각선을 타고 아래로 내려가는 i의 범위 또한 좁아진다.

j=i+L이므로 자동 지정되며, 표에서는 열에 해당된다. C[i,j] 셀은 L대각선의 i번째 행에 위치해있다. 위 그림 좌측에서 빨간색으로 칠해진 셀이 C[3,4]셀이다. L=1, i=3인 상황.

여기까지 L,i 루프를 통해 특정 셀을 지정하였다. 이후 k루프에서는 연산 최소값을 비교해야하니 해당 셀 C[i,j]의 값을 INF로 초기화 하였다.

k 루프

본 알고리즘이 DP 알고리즘으로 분류되는 원인이 이것이다. 사전에 구해둔 최소 연산 횟수를 사용하여 해당 셀의 값을 구하기 때문. 코드에서 C[i,j]를 구하기 위하여 C[i,k], C[k+1,j]를 사용하는 모습이다.

k는 구하고자 하는 행렬을 두 행렬으로 구분하기 위한 번호이다. 예를들어 셀 C[1,4]는 AxBxCxD의 최소 연산 횟수를 담고 있다. 이를 두 행렬의 곱으로 표현하면 아래 그림처럼 Ax(BCD), (AB)x(CD), (ABC)xD로 나타낼 수 있다. 이들 중 연산 횟수가 가장 작은 값을 구하면 된다.

표에서 C[1,4]를 구하기 위해 각 k에서 사용되는 C[i,k], C[k+1,j] 위치를 참고하자.

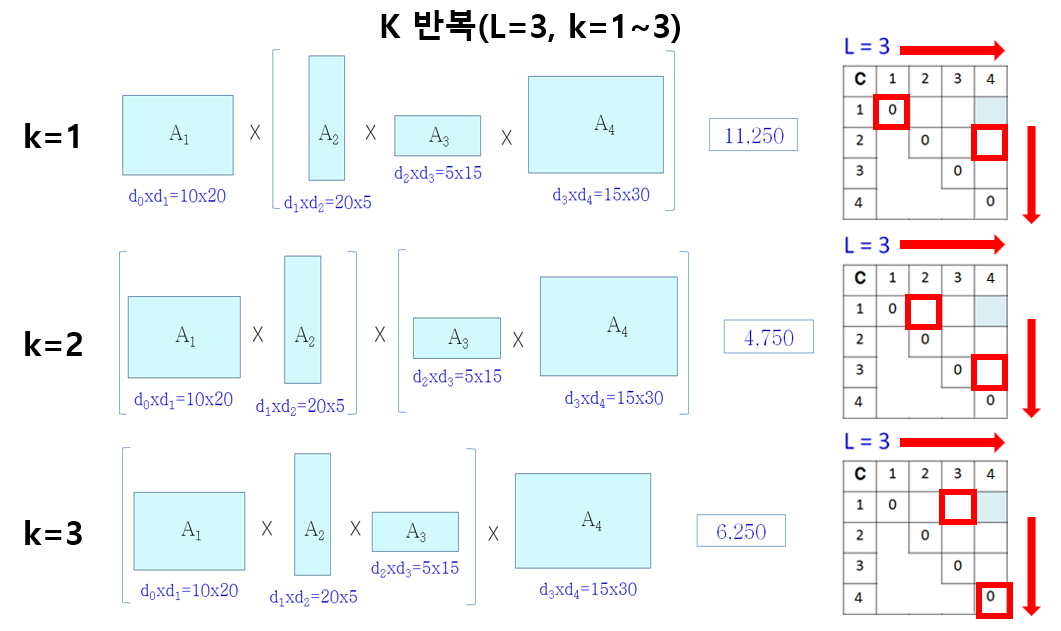
k값 마다 아래의 식을 따라 연산을 진행한다. C[i,k], C[k+1,j]값은 앞서 미리 연산이 진행되어 최솟값으로 채워져있다. 그러니 두 값을 가져와서 더하고, 추가로 두 행렬 곱셈의 연산값을 더하면 해당 k값을 기준으로 나눈 두 행렬의 연산 횟수가 나오는 것이다.

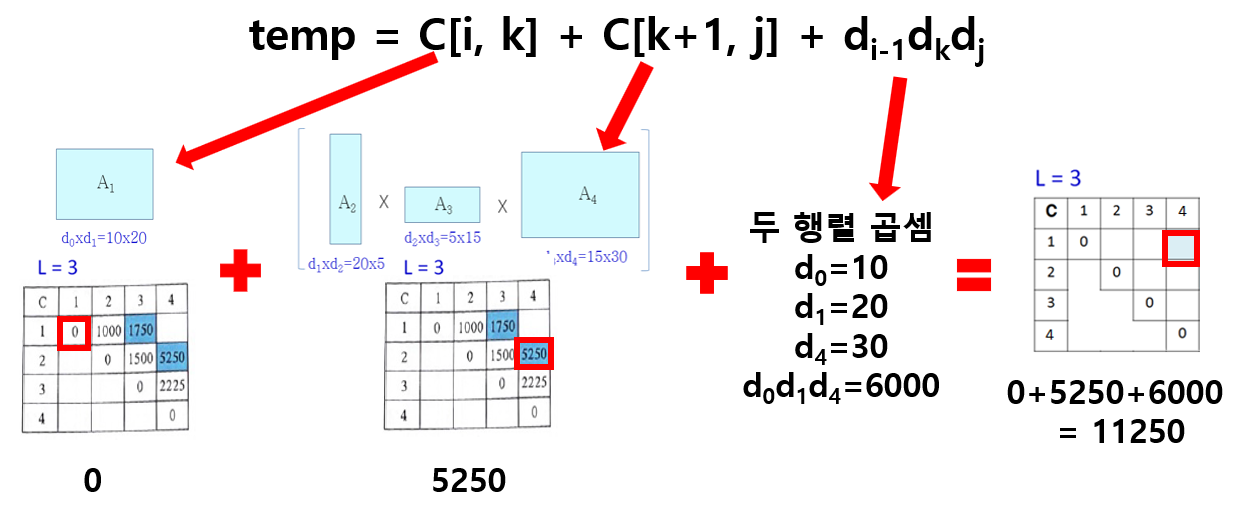
최종적으로 C[1,N]을 얻을 수 있다!!

참고 도서

• 양성봉, 『알기 쉬운 알고리즘』. 파주: (주)생능출판사, 2013